TestDoc
TestDoc
这是一篇测试文章,选用的内容为数学建模插值的内容:
插值
[toc]
一、插值定义
数据处理问题:在平面上给定一组离散点列,要求一条曲线把这些点依次连接起来,称之为插值
注意!此部分出现了大量不同的有关矩阵的函数运算方法,不同的运算方法之间对行标和列标的对应不同,最好在使用之前用size()方法看清相应的大小和对应关系,再进行操作!
二、常见插值方法
已知$n+1$个点$(x_i,y_i)\ (i=0,1,…,n)$,下面求各种插值函数
(一)分段线性插值
将两个相邻的节点用直线连接起来,如此形成的一条折线就是分段线性插值函数,记作$In(x)$,它满足$I_n(x_i)=y_i$,且$I_n(x)$在每一个小区间$[x_i,x{i+1}]$上是线性函数 $(i=0,1,…,n)$
$In(x)$可以表示为$I_n(x)\sum\limits^n{i=0}y_il_i(x)$,其中
$I_n(x)$有较好的收敛性,即对于$x\in[a,b]$,有
用$I_n(x)$计算x点的插值时,只用到x左右的两个节点,计算量与节点个数n无关。但n越大,分段越多,插值误差越小。实际上用函数表做插值计算时,分段线性插值就足够了,如:数学、物理重用的特殊函数表,数理统计中用的概率分布表等等
(二)拉格朗日插值多项式
拉格朗日插值的基函数为
其中$l_i(x)$是n次多项式,满足
i,j相同时,$l_i(x)$式上下一致,结果为1
i,j不同时,$li(x)$中一定存在$(x_j-x?)=0$,结果为0
拉格朗日插值函数:
(三)样条插值
部分问题对所得插值函数的光滑性有较高的要求,不仅要连续,而且要有连续的曲率
样条(Spline)原指富有弹性的细木条或金属条。利用将已知点连接成一条光滑曲线(称为样条曲线),并使连接点处具有连续的曲率,三次样条插值就是如此抽象出来的
数学上将具有一定光滑性的分段多项式称为样条函数。具体来说,给定区间[a,b]的一个分划
如果函数S(x)满足
- 在每一个小区间$[xi,x{i+1}]\ (i = 0,1,\cdots,n-1)$上S(x)是m次多项式
- S(x)在$[a,b]$上具有m-1阶连续导数
则称S(x)为关于分划$\Delta$的m次样条函数,其图形为m次样条曲线。显然,折现是依次样条曲线
三、MATLAB插值工具箱:notebook_with_decorative_cover:
(一)一维插值函数 interp1()
Code : <ValName> = interp1(x0, y0, x, <method>)
其中<method>指插值的方法,默认为线性插值(‘linear’),其可选值有:
| < method > | Description | Sp |
|---|---|---|
| ‘linear’ | 线性插值 | None |
| ‘nearest’ | 最近项目插值 | None |
| ‘spline’ | 立方(三次)样条插值 | 保证函数平滑 |
| ‘cubic’ | 立方(三次)插值 | 保持函数凸凹性 |
其中所有的插值方法都要求x0是单调的
当x0为等距的时候可以使用快速插值法
method格式:
'*linear','*nearest','*spline','*cubic'
(二)一维三次样条插值
CodeStyle01 : <ValName> = interp1(x0, y0, x, 'spline')
CodeStyle02 : <ValName> = spline(x0, y0, x)
Recommand : csape()
CodeStyle03 : pp = csape(x0, y0, <conds>)
<ValName> = fnval(pp, x)
CodeStyle04 : pp = csape(x0, y0, <conds>, <valconds>)
<ValName> = fnval(pp, x)
提倡使用函数csape,其返回值是pp形式,为了求出插值点的函数值,需要调用函数fnval
pp = csape(x0, y0)使用默认的边界条件(Lagrange边界条件)
<conds>为指定插值的边界条件,可选值如下
< conds > Description < valconds > ‘complete’ 边界为一阶导数 需提供 ‘not-a-knot’ 非扭结条件 ‘periodic’ 周期条件 ‘second’ 边界为二阶导数(缺省值为[0,0]) 需提供 ‘variational’ 设置边界的二阶导数值为[0,0] 对于一些特殊的边界条件,可以通过conds的一个1$\times$2矩阵来表示,conds元素的取值为0,1,2 Eg:
conds = [2,1]左边界是二阶导数,右边界是一阶导数,相应的值由valconds给出
<valconds>为<conds>方法所需的值,若不填写则按照缺省情况处理
(三)二维插值
1. 插值节点为网格节点
已知m$\times$n个节点:$(xi,y_j,z{ij})\ (i = 1,2,\cdots,m;\ j=1,2,\cdots,n)$,
且$x_1<\cdots<x_m;\ y_1<\cdots<y_n$
求点$(x, y)$处的插值
(1)二维插值函数
Code : <ValName> = interp2(x0, y0, z0, x, y, <method>)
其中<method>指插值的方法,同一维的参数相同
x0,y0分别为m维和n维向量,表示节点,z0为n$\times$m维度矩阵,表示节点的值,x,y为一维数组,指插值点,
x与y应当是方向不同的向量,即一个是行向量,一个是列向量(y需要转置)
输出内容为矩阵,Row=y的维数,Col=x的维数,表示得到的插值
(2)二维三次样条插值
Code : pp = csape({x0, y0}, z0, conds, valconds)
<ValName> = fnval(pp, {x, y})
对其内容的解释同上
(3)显示相应的三维网格图
Code : mesh(y,x,z)
mesh函数的x为列,y为行,需要将xy反写
2. 插值节点为散乱节点
已知n个节点$(x_i,y_i,z_i)\ (i=1,2,\cdots,n)$,求点$(x,y)$处的插值z
Code:<ValName> = griddata(x, y, z, XI, YI)
其中x、y、z均为n维向量,指明所给出数据的横坐标、纵坐标和竖坐标
向量XI、YI是给定的网格点的横坐标和纵坐标
返回值<ValName>为网格(XI, YI)处的函数值,但是行为YI,列为XI,进行mesh的时候不需要反转XY
XI与YI应当是方向不同的向量,一行一列(YI需要转置)
MATLAB中插值时,外插值是不确定的,可以使用混合插值的方法,把不确定的插值换成最近点的插值结果
2
3
4
ZI2=griddata(x,y,z,XI,YI','nearest'); %最近点插值
ZI = ZI1; %
ZI(isnan(ZI1)) = ZI2(isnan(ZI1));
四、实战例题
Eg5.1 机床加工
待加工零件的外形根据工艺要求由一组数据$(x,y)$给出(在平面情况下),用程控铣床加工时每一刀只能沿$x$方向和$y$方向走非常小的一步,这就需要从已知数据得到加工所要求的步长很小的$(x,y)$坐标。
Data中给出的$x,y$数据位于机翼断面的下轮廓线上,假设需要得到$x$坐标==每改变0.1时==的$y$坐标。试完成加工所需数据,==画出曲线==,并==求出$x=0$处的曲线斜率和$13\le x\le15$范围内y的最小值==。要求用==分段线性==和==三次样条==两种插值方法计算。
Data:
| x | 0 | 3 | 5 | 7 | 9 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 0 | 1.2 | 1.7 | 2.0 | 2.1 | 2.0 | 1.8 | 1.2 | 1.0 | 1.6 |
1 | clear |
output
1 | k(0) = 0.49716 |
Pic

Eg5.2 求速度曲线的位移
已知速度曲线$v(t)$上的四个数据点如下表,用三次样条插值求位移
Data:
| $t$ | 0.15 | 0.16 | 0.17 | 0.18 |
|---|---|---|---|---|
| $v(t)$ | 3.5 | 1.5 | 2.5 | 2.8 |
1 | clear |
output
1 | xs = -616666.666666667 33500 -473.333333333334 3.5 |
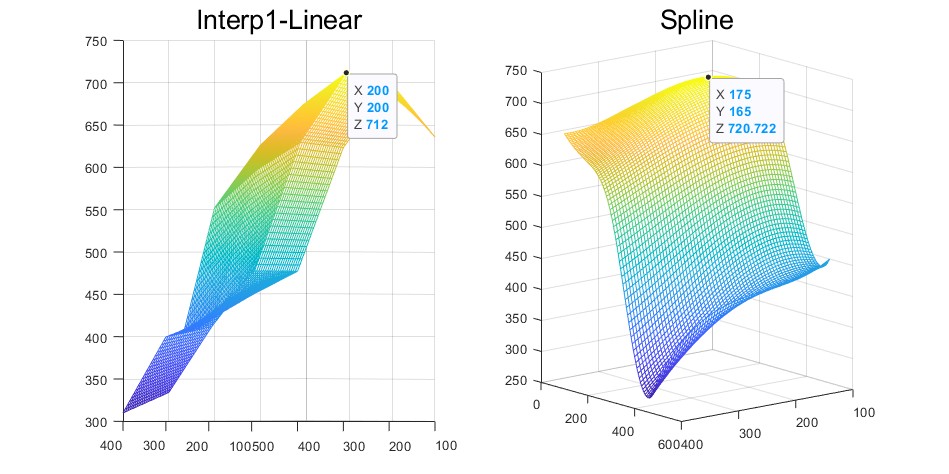
Eg5.3 丘陵曲面最高点
在一丘陵地带测量高程,==x和y方向每隔100米==测一个点,得高程如表,试插值一==曲面==,确定合适的模型,并由此找出==最高点和该点的高程==
Data:
| y\x | 100 | 200 | 300 | 400 | 500 |
|---|---|---|---|---|---|
| 100 | 636 | 697 | 624 | 478 | 450 |
| 200 | 698 | 712 | 630 | 478 | 420 |
| 300 | 680 | 674 | 598 | 412 | 400 |
| 400 | 662 | 626 | 552 | 334 | 310 |
注意此处直接列写矩阵,则xy与正常的对应相反
1 | clear |
output
1 | 720.7217 165.0000 175.0000 |
Pic
Eg5.4 海底图像
在某海域测得一些点(x,y)处的水深z由表5.4给出,在适当的矩形区域内画出海底曲面的图形。
Data:
x=[129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
y=[7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
z=-[4,8,6,8,6,8,8,9,9,8,8,9,4,9];
1 | clear |
Pic



