评价模型

一、层次分析法 AHP

学习源Video:Bilibili-ln异教徒 AHP

作用：层次分析法用来进行决策，求指标的权重

模型建立步骤：

  • 建立层次结构

    • 将决策问题分为三个部分：目标层、准则层和指标层/方案层

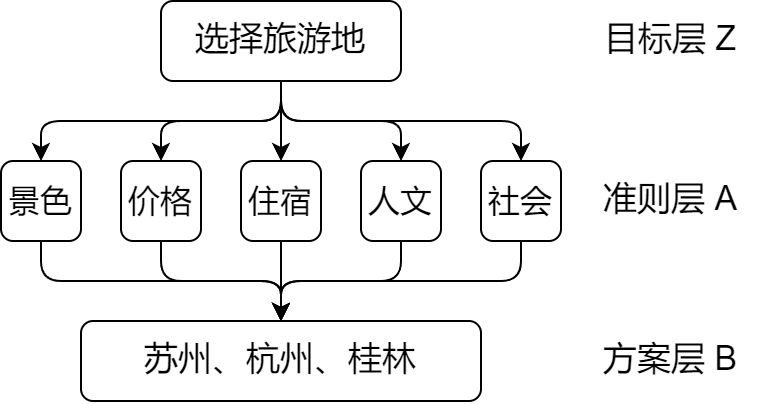
  • 对准则层构建判断矩阵

    • 判断矩阵为两两指标重要性的判断，一般判别矩阵构造如下：

    九级标度法表格

    | 标度 | 含义 |
    | ———————— | ————————————————————- |
    | 1 | i和j具有相同的重要性(Eg:主对角线元素) |
    | 3 | i比j稍微重要 |
    | 5 | i比j明显重要 |
    | 7 | i比j强烈重要 |
    | 9 | i比j极端重要 |
    | 2、4、6、8 | 上述标度的中间量 |
    | $\frac{1}{标度}$ | 矩阵下三角对称位置的值 |

  • 一致性检验（特征根法）

    在通过主观想法确定两个属性之间的重要性差距标度时，可能出现不一致的情况，需要用一致性检验对所得的判断矩阵进行一致性的检验，确定所得的判断矩阵能够使用

    一致性的例子：A~12~=2, A~13~=2,那么说明1 对 2和3 的重要程度相同，可以推出2和3的重要程度相同，

    ​ 即A~23~ = A~32~ =1，如果该值不为1则说明其不一致。

    用对应于A的最大特征根（记为$\lambda$）的特征向量（归一化后）作为权向量$w$，即$w$满足

    当 $\lambda = n$ 时，该判断矩阵为一致阵，且任何判断矩阵的最大特征根 $\lambda\ge n$ 。因此，当最大特征根比 $n$ 大得多时，该判断矩阵的不一致程度越严重，所以可以用 $\lambda - n$ 的数值来衡量判断矩阵的不一致程度，并将

    作为一致性指标，当$CI=0$时判断矩阵为一致阵，并引入随机一致性指标$RI$，$RI$数值如下：

$n$ 3 4 5 6 7 8 9
$RI$ 0.58 0.9 1.12 1.24 1.32 1.41 1.45

将它的一致性指标$CI$与同阶（指$n$相同）的随机一致性指标$RI$之比称为一致性比率$CR$，当

时，认为该判断矩阵的不一致程度在容许范围之内，可以用其特征向量作为权向量。最终得到每个指标的权重结果。

    • 方法一：使用MATLAB的eig()方法直接求得特征根 $v$和特征向量$d$，随后通过求取特征向量和特征值的所在列，计算w = v(:,loc)/sum(v(:,loc));得到转为行向量，即权向量res_A。

​ Matlab-ModelCode

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
clear
clc
%% 判断矩阵导入
A = [1   1/4 1/4 2 2
     4   1   1   6 6
     4   1   1   6 6
     1/2 1/6 1/6 1 1
     1/2 1/6 1/6 1 1]
%% 一致性检验
n = length(A);
[v, d] = eig(A); % 计算特征根和特征向量
[temp, loc] = max(max(d)); % 返回loc为特征向量的所在列
r = temp; % 得到lambda_max的值
CI = (r-n)/(n-1); % 计算一致性指标CI
RI = [0 0 0.58 0.90 1.12 1.24 1.32 1.41 ... % 换行输入
      1.45 1.49 1.52 1.54 1.56 1.58 1.59]; % 引入随机一致性指标RI
CR = CI/RI(n); % 计算一致性比率CR
if CR < 0.1 || n == 2 % 确定其一致性比率<0.1或只含有两个元素，两个元素一定一致
    CR_Result = 'Pass';
else
    CR_Result = 'Nope';
end
%% 权向量计算
w = v(:,loc)/sum(v(:,loc));
w = w';
%% DispResult
disp('---------AHP---------')
disp(['CI: ' num2str(CI)]) % 一致性指标
disp(['CR: ' num2str(CR)]) % 一致性比率
disp(['CR_Result: ' num2str(CR_Result)]) % 一致性检验结果
if CR_Result == 'Pass' % 若一致性检验通过则输出特征值和权向量
    disp(['lambda: ' num2str(r)]) % 特征值
    disp(['w: ' num2str(w)]) % 权向量
end
    • 方法二：算术平均法求权重

将判断矩阵按照列归一化$\to$将归一化的结果按行求和$\to$每个元素除以n

  • 对指标层/方案层的内容构建
    • 每一个准则层性质中 多个指标间的判断矩阵并进行AHP（多个准则，每个准则指向多个指标）
    • 每一个准则层性质的 每个方案间的判断矩阵并进行AHP（多个准则，多个主责指向多个方案）
  • 将准则层/方案层的每一个准则性质的$w$转成行向量
    • 准则层的所有值$w$值构成权向量res_B
    • 方案层纵向拼接，所得的即为方案曾的权矩阵res_B，
  • 计算最终得分/综合权重
    • 指标：res_A(指标层集的大类准则)$\times$res_B所得结果
    • 方案：res_A$\times$res_B得到综合权重res_Z

二、熵权法 EWM

学习源Video:Bilibili-ln异教徒 EWM

  • 数据的归一化处理

    由于各项指标计量单位并不统一，因此在计算综合权重前先要对它进行标准化处理，即把指标的绝对值转化为相对值，并令 $x{\small ij} = |x{\small ij}|$ ，从而解决各项不同质指标的同质化问题。

    • 方法一：

      由于正向指标和负向指标数值代表的含义不同（正向指标数值越高越好，负向指标数值越低越好），因此对于高低需求指标应当采取不同的算法进行数据标准化处理，具体处理方法为 :

      对于正向指标：

      对于负向指标：

通常会采用一些稍微小一点的值来代替 0 和 1，以便更好地保留原始数据的分布特征。

且直接使用 0 和 1 作为归一化后的极值，可能会导致数据过于集中在边界附近，失去了部分信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
% Matlab的归一化自定义函数 # Gy.m
function y = Gy(x,type,ymin,ymax)
% 实现正向或负向指标归一化，返回归一化后的数据矩阵
% x为原始数据矩阵，一行代表一个样本，每列代表一种指标
% type设定正向指标1，负向指标2
% ymin，ymax为归一化的区间端点
[n, m] = size(x);
y = zeros(n,m);
xmin = min(x);
xmax = max(x);
switch type
    case 1
        for j=1:m
            y(:,j)=(ymax-ymin)*(x(:,j)-xmin(j))/(xmax(j)-xmin(j))+ymin;
        end
    case2
        for j=1:m
            y(:,j)=(ymax-ymin)*(xmax(j)-x(:,j))/(xmax(j)-xmin(j))+ymin;
        end
end
end

  • 方法二：Python scikit-learn MinMaxScaler

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    # 数据归一化(sklearn)
    import numpy as np
    import pandas as pd
    from sklearn.preprocessing import MinMaxScaler
    data = [[1,2,3],
            [4,5,6],
            [7,8,9],]
    # 如果data为单列则需添加.values.reshape(-1,1)
    print('data:',data[:5]) # 展示前五个数据

    MM_Scaler = MinMaxScaler(feature_range=(0,1)) # 默认缩放范围(0,1)
    MMres = MM_Scaler.fit_transform(data)
    print('MMres:',np.round(MMres[:5,],2)) # 展示前五个数据,保留3位小数

  • 计算第$j$项指标下第$i$方案指标值的比重$p_{ij}$

  • 计算第$j$项指标的熵值$e_j$

    其中$k=\dfrac{1}{\ln(n)}$，满足$e_j\ge 0$

  • 计算信息熵冗余度$g_{j}$

  • 计算各项指标权重$w_j$

  • 计算综合评分$S_i$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
clear
clc
%% DataLoad
data = xlsread('./HouseData.xlsx');
%% 归一化
ind = ones(size(data,2),1); % data列数作为RowCount,ColCount=1
% indArr的建立，正向写1，负向写2，在此处默认都是正向指标，所以建立全一的纵向Arr

[n, m] = size(data); % n个样本，m个指标
for j = 1:m
    if ind(j) == 1 % 正向指标的归一化
        X(:,j) = Gy(data(:,j),1,0.002,1); % 归一化最低值范围不能为0

    else % 负向指标的归一化
        X(:,j) = Gy(data(:,j),2,0.002,1);
    end
end
%% 熵权法求取权向量
% 计算第j个指标下，第i个样本占该指标的比重p(i,j)
for i = 1:n
    for j = 1:m
        p(i,j) = X(i,j)/sum(X(:,j));
    end
end
% 计算第j个指标的熵值e(j)
k = 1/log(n);
for j = 1:m
    e(j) = -k * sum(p(:,j).*log(p(:,j)));
end
g = ones(1,m)-e; % 计算信息熵冗余度
w = g./sum(g); % 求权值w
s = X*w'; % 求综合评分
% DispPlot
disp('Gyed_Data:');disp(X)
disp('p(i,j):');disp(p)
disp('e(j):');disp(e)
disp('g(j):');disp(g)
disp('w(j):');disp(w)
disp('s(j):');disp(s)
plot(2017:-1:2010,s)